Πρόβλημα 1
Έστω οξυγώνιο τρίγωνο και έστω
και έστω  ο περιγεγραμμένος κύκλος του. Τα σημεία
ο περιγεγραμμένος κύκλος του. Τα σημεία  και
και  βρίσκονται στα τμήματα
βρίσκονται στα τμήματα  και
και  αντίστοιχα ώστε
αντίστοιχα ώστε  .
.
Οι μεσοκάθετες των και
και  τέμνουν τα μικρά τόξα
τέμνουν τα μικρά τόξα  και
και  του
του  στα σημεία
στα σημεία  και
και  αντίστοιχα.
αντίστοιχα.
Να αποδειχθεί ότι οι ευθείες και
και  είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
Έστω πως η τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  σε σημείο
σε σημείο  .
.
Παρατηρούμε πως .
.
Άρα το τρίγωνο είναι ισοσκελές, με
είναι ισοσκελές, με  .
.
Όμοια αν η τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  στο
στο  , τότε
, τότε  .
.
Θα αποδείξουμε πως , δηλαδή
, δηλαδή  .
.
Παρατηρούμε πως , ενώ
, ενώ  (εφόσον η
(εφόσον η  είναι επίκεντρη της
είναι επίκεντρη της  στο κύκλο με κέντρο
στο κύκλο με κέντρο  και ακτίνα
και ακτίνα  .
.
Άρα αρκεί να αποδείξουμε πως , δηλαδή
, δηλαδή  .
.
Ξέρουμε όμως πως , από τον ορισμό του
, από τον ορισμό του  .
.
Άρα αρκεί .
.
Παρατηρούμε πως το τετράπλευρο είναι εγγράψιμο και
είναι εγγράψιμο και  , άρα η
, άρα η  είναι η διχοτόμος της
είναι η διχοτόμος της 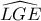 .
.
Αν το δεν ήταν ισοσκελές, τότε αφού το
δεν ήταν ισοσκελές, τότε αφού το  ανήκει στη διχοτόμο της
ανήκει στη διχοτόμο της 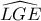 και
και  , θα έπρεπε το
, θα έπρεπε το  να είναι εγγράψιμο (θεώρημα νότιου πόλου), άτοπο, αφού ο περιγεγραμμένος κύκλος του
να είναι εγγράψιμο (θεώρημα νότιου πόλου), άτοπο, αφού ο περιγεγραμμένος κύκλος του  είναι ο περιγεγραμμένος κύκλος του
είναι ο περιγεγραμμένος κύκλος του  και το
και το  δεν ανήκει σε αυτό το κύκλο.
δεν ανήκει σε αυτό το κύκλο.
Άρα το είναι ισοσκελές με
είναι ισοσκελές με  και το ζητούμενο έπεται.
και το ζητούμενο έπεται.
https://mathematica.gr/
Έστω οξυγώνιο τρίγωνο
 και έστω
και έστω  ο περιγεγραμμένος κύκλος του. Τα σημεία
ο περιγεγραμμένος κύκλος του. Τα σημεία  και
και  βρίσκονται στα τμήματα
βρίσκονται στα τμήματα  και
και  αντίστοιχα ώστε
αντίστοιχα ώστε  .
.Οι μεσοκάθετες των
 και
και  τέμνουν τα μικρά τόξα
τέμνουν τα μικρά τόξα  και
και  του
του  στα σημεία
στα σημεία  και
και  αντίστοιχα.
αντίστοιχα.Να αποδειχθεί ότι οι ευθείες
 και
και  είτε είναι παράλληλες είτε είναι οι ταυτόσημες.
είτε είναι παράλληλες είτε είναι οι ταυτόσημες.Έστω πως η
 τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  σε σημείο
σε σημείο  .
.Παρατηρούμε πως
 .
.Άρα το τρίγωνο
 είναι ισοσκελές, με
είναι ισοσκελές, με  .
.Όμοια αν η
 τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  στο
στο  , τότε
, τότε  .
. Θα αποδείξουμε πως
 , δηλαδή
, δηλαδή  .
.Παρατηρούμε πως
 , ενώ
, ενώ  (εφόσον η
(εφόσον η  είναι επίκεντρη της
είναι επίκεντρη της  στο κύκλο με κέντρο
στο κύκλο με κέντρο  και ακτίνα
και ακτίνα  .
.Άρα αρκεί να αποδείξουμε πως
 , δηλαδή
, δηλαδή  .
.Ξέρουμε όμως πως
 , από τον ορισμό του
, από τον ορισμό του  .
. Άρα αρκεί
 .
.Παρατηρούμε πως το τετράπλευρο
 είναι εγγράψιμο και
είναι εγγράψιμο και  , άρα η
, άρα η  είναι η διχοτόμος της
είναι η διχοτόμος της 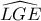 .
.Αν το
 δεν ήταν ισοσκελές, τότε αφού το
δεν ήταν ισοσκελές, τότε αφού το  ανήκει στη διχοτόμο της
ανήκει στη διχοτόμο της 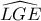 και
και  , θα έπρεπε το
, θα έπρεπε το  να είναι εγγράψιμο (θεώρημα νότιου πόλου), άτοπο, αφού ο περιγεγραμμένος κύκλος του
να είναι εγγράψιμο (θεώρημα νότιου πόλου), άτοπο, αφού ο περιγεγραμμένος κύκλος του  είναι ο περιγεγραμμένος κύκλος του
είναι ο περιγεγραμμένος κύκλος του  και το
και το  δεν ανήκει σε αυτό το κύκλο.
δεν ανήκει σε αυτό το κύκλο.Άρα το
 είναι ισοσκελές με
είναι ισοσκελές με  και το ζητούμενο έπεται.
και το ζητούμενο έπεται. https://mathematica.gr/
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου